| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | ||||||
| 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| 16 | 17 | 18 | 19 | 20 | 21 | 22 |
| 23 | 24 | 25 | 26 | 27 | 28 | 29 |
| 30 |
- 재테크
- 화장품
- 지혜를가진흑곰
- 알고리즘트레이닝
- 돈
- 백준알고리즘
- 알고리즘공부
- algorithmTest
- Java
- JavaScript
- 책을알려주는남자
- C++
- algorithmStudy
- C
- 책알남
- 독서
- 독후감
- 프로그래밍언어
- 자바
- 성분
- 주식
- 알고리즘 공부
- 자바스크립트
- algorithmtraining
- 경제
- 서평
- 채권
- 투자
- 프로그래머스 알고리즘 공부
- 다독
- Today
- Total
탁월함은 어떻게 나오는가?
[Algorithm] 최장 공통 부분 수열(Longest Common Subsequence)로 공부하는 동적 프로그래밍(Dynamic Programming) 본문
[Algorithm] 최장 공통 부분 수열(Longest Common Subsequence)로 공부하는 동적 프로그래밍(Dynamic Programming)
Snow-ball 2025. 1. 1. 11:52오늘은 LCS 알고리즘을 공부해보겠다.
LCS 문제는 두 문자열의 부분 수열을 비교하는 문제로, DP를 활용하여 해결하는 문제이다.
DP를 사용하는 이유
LCS 문제에서 DP가 적절한 이유는 중복되는 부분 문제와 최적 부분 구조를 가지기 때문이다.
1. 중복되는 문제
- 두 문자열을 비교하다 보면, 같은 부분 문자열을 여러 번 계산하게 된다. 예를 들어, DP배열을 사용하지 않는다면 dp[i][j]를 계산할 때 dp[i - 1][j - 1], dp[i - 1][j], dp[i][j - 1] 같은 부분을 반복적으로 계산해야 한다.
- DP는 이러한 중복 계산을 한 번만 계산하고 저장하여, 다시 계산하지 않도록 하는게 큰 아이디어이다. 이로 인해서 계산량을 크게 줄일 수 있다.
2. 최적 부분 구조
- 부분 문제들의 최적 해를 결합하여 전체 문제의 최적 해를 찾을 수 있는 구조를 가지고 있다.
- 예를 들어, 두 문자열의 LCS를 구할 때, 부분 문자열들의 LCS를 먼저 구하고 그 값을 이용해 전체 문자열의 LCS를 계산한다. 즉, dp[i][j] 는 dp[i - 1][j - 1], dp[i - 1][j], dp[i][j - 1] 의 최적 값을 조합하여 구한다.
DP의 장점
1. 효율성: DP를 사용하면 중복 계산을 줄이고, 최종 결과를 효율적으로 구할 수 있다. 재귀적으로 풀 때 계산량이 O(2^n) 만큼 계산량이 증가하지만, DP는 이 문제를 O(m x n) 시간 복잡도로 해결할 수 있다. (m과 n은 두 문자열의 길이)
2. 문제의 구조에 맞는 해결법: DP는 부분 문제의 해결을 기반으로 최종 문제를 해결하므로 LCS와 같은 최적화 문제에서 매우 적합하다.
3. 메모리 절약: DP를 사용하면 이전에 계산한 값들을 저장하여 불필요한 중복 계산을 피할 수 있다. DP 배열을 한 번만 채우면 되므로 시간 복잡도도 O(m x n)로 줄어든다.
풀이
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
|
def lcs(X, Y):
m = len(X)
n = len(Y)
dp = [[0] * (n + 1) for _ in range(m + 1)]
# 2중 포문을 돌면서 DP 테이블 채우기
for i in range(1, m + 1):
for j in range(1, n + 1):
if X[i - 1] == Y[j - 1]: # 문자가 일치하면
dp[i][j] = dp[i - 1][j - 1] + 1
else: # 문자가 다르면
dp[i][j] = max(dp[i - 1][j], dp[i][j - 1])
return dp[m][n]
X = "AGGTAB"
Y = "GXTXAYB"
print(lcs(X, Y)) # Output: 4
|
cs |
풀이 설명
dp 배열은 4라인에서 세팅을 하면 다음과 같이 모든 값이 0으로 초기화가 된다.
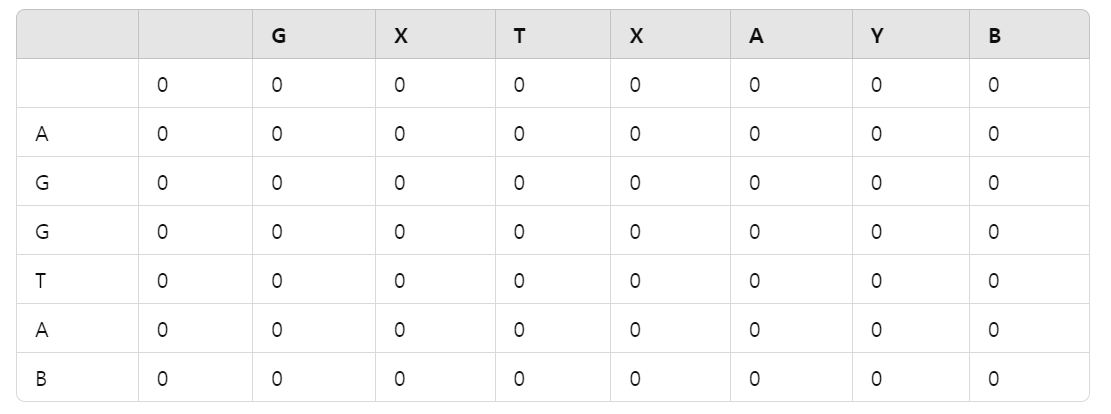
i = "AGGTAB" 이므로 A, G, G ... B 를 출력, J = "GXTXAYB" 이므로 G, X, T ... B 까지 출력한다.
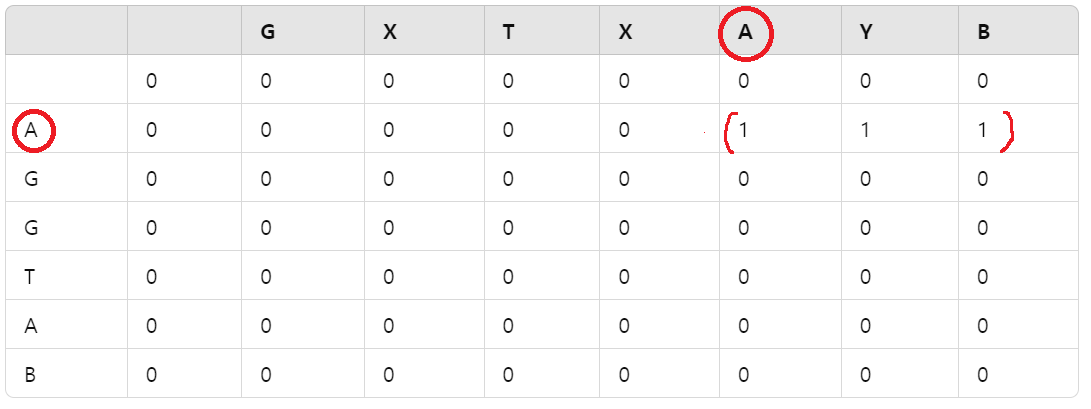
위의 테이블을 보면 열의 i를 의미하고 행이 j를 의미하게 된다.
2중 포문을 돌다가 i = 1, j = 5이 되면 둘다 A이기 때문에 숫자 1이 증가된다. dp[1][5] = 1 이 되고, 이후의 dp[1][6], dp[1][7] 또한 1이 된다.
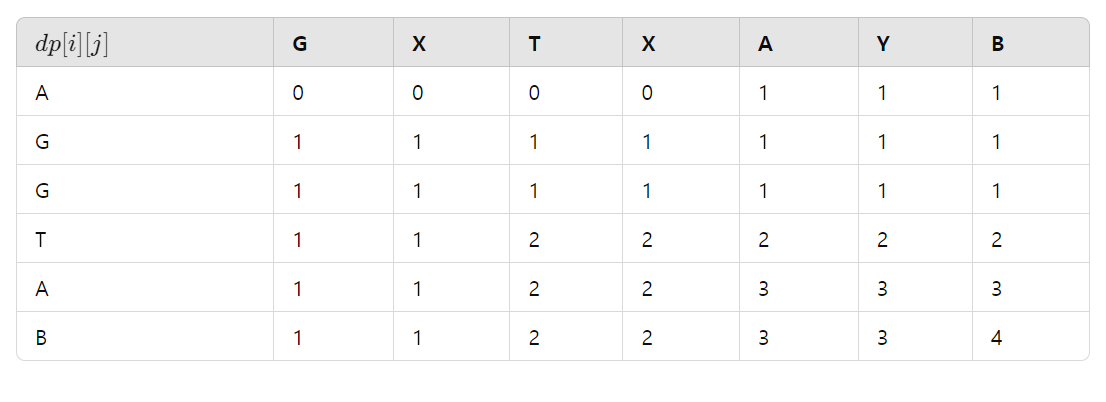
최종적으로는 dp 배열이 다음과 같이 채워지는걸 확인할 수 있게 된다.
'[Snow-ball]프로그래밍(컴퓨터) > Algorithm' 카테고리의 다른 글
| [Algorithm] 동전 교환 문제(Coin Change Problem)로 공부하는 동적 프로그래밍(Dynamic Programming) (1) | 2024.12.29 |
|---|---|
| [Algorithm] 혼자서 하는 틱택토 ( Programmers / Python ) (0) | 2024.06.11 |
| [Algorithm] 달리기 경주 (JavaScript - Programmers) (0) | 2023.04.11 |
| [Algorithm] 욕심쟁이 알고리즘 배낭무게 문제풀이 [C++] (0) | 2022.04.28 |
| [algorithm 이론] for문 사용할때 i++, ++i는 어떤 차이가 있을까? (0) | 2022.03.16 |



